Frossky 发布的文章
Android文件管理器选择
本来用了多年的ES文件管理器,最近总是弹出一个广告, 弹出也就罢了, 关闭按钮给的黑小还有给了一真一假两个, 每次都按错. 心想这么多年买个会员吧, 定价又有点儿超预期😅
然后评测了其他的文件管理器, 需要G Play下载
- Total Commander. 老牌管理器了, 不过默认版本不支持SMB, 还需要额外下载插件, UI体验不好.
- Amaze File Manager. alternativeto高分推荐, 不过却不支持SMB.
- File Commander. 还不错, 有广告但只在最下面.
- CX文件管理器. 非常好, 没有广告, 支持SMB.
使用python与命令行程序交互
找了好久, 一开始的方案是 subprocess.Popen, 结果发现能收不能发, 能发不能收. 很郁闷.
发的代码:
import subprocess
import time
proc = subprocess.Popen(["a.exe"], stdin=subprocess.PIPE)
p=proc
p.stdin.write(b'asdf')
time.sleep(1)
p.stdin.write(b'2q3w')
p.stdin.write(b'zxcv')
p.communicate()
p.wait() # wait for the subprocess to exit
print("py finished")收的代码:
import subprocess
import time
proc = subprocess.Popen(["a"], stdout=subprocess.PIPE)
p=proc
with p.stdout:
for line in iter(p.stdout.readline, b''):
print(line)
p.wait() # wait for the subprocess to exit
print("py finished")
直到有位大哥提到了Pexpect这个库. 以及envoy和sarge. https://stackoverflow.com/questions/10872767/differences-between-subprocess-module-envoy-sarge-and-pexpect
- pexpect doc, on pypi, Released: Jan 22, 2020
- envoy, Released: Aug 13, 2014
- sarge doc, sarge pypi, Released: Dec 12, 2021
node的expect版本也有, 叫做node-suppose
sarge
发现sarge是比较好的解决方案:
import sys
from time import sleep
from sarge import Feeder, run, Capture
feeder = Feeder()
p = run(['a'], input=feeder, stdout=Capture(), async_=True)
sleep(1)
feeder.feed('Hello')
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
sleep(1)
feeder.feed('Yes')
sleep(1)
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
feeder.feed('Man')
sleep(1)
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
print(p.stdout.readline())
feeder.close()
p.close() 监控键盘输入
开源如何商业化?
引用文章
讲述MongoDB的开源许可证: [开源许可证,欢迎来到云时代]()https://3g.163.com/dy/article/HEHAH8HU0511CUMI.html)
开源软件许可证类型完整指南 2020
开源许可证分类
首先看是否是OSI(Open Source Initiative)认证的许可证, 包括: GPL MPL LGPL AGPL MIT BSD Apache. 其他, 包括SSPL(APGL + Common Clause), Elastic License V2.
在OSI之下, 分为Copyleft(著佐权)和Permissive(宽松许可证).
Copyleft会要求基于本软件的代码也要开源, Permissive则无此要求.
Copyleft包括GPL, 轻度Copyleft包括 CDDL MPL Eclipse.
Permissive包括MIT BSD Apache.
许可证排名
MIT Apache GPL
MIT
也称为X许可证或者X11许可证
MIT内容与条款3伯克利许可证(3-clause BSD license)内容颇为近似,但是赋予软件被授权人更大的权利与更少的限制。
- 被授权人有权利使用、复制、修改、合并、出版发行、再授权及出售软件及软件的副本。
- 被授权人可根据程序的需要修改授权条款为适当的内容。
- 在软件和软件的所有副本中都必须包含版权声明和许可声明。
- MIT的内容可依照程序著作权者的需求更改内容。此亦为MIT与BSD(The BSD license, 3-clause BSD license)本质上不同处。
- MIT条款可与其他授权条款并存。另外,MIT条款也是自由软件基金会(FSF)所认可的自由软件授权条款,与GPL兼容。
Apache
Apache 许可证2.0和GNU GPL之间的区别
GNU GPL是一个著佐权许可证。因此,使用GPL许可证组件的软件,必须发布其源代码,和所有修改及发行整个源代码的权利。Apache 许可证2.0 不强制这样的条款,不强制你发布修改过的版本。此外,你能选择使用不同的许可证发布你修改过的版本(然而,对未被修改过的代码,要求你保留Apache 许可证)。
GPL中不包含特定的要求(这个要求指对程序做广告)。在Apache2.0和伯克利之间的区别
伯克利许可证是另一个高度宽松许可证,允许你修改和按照自己的意愿选择许可证,并再发行伯克利许可证下软件。早期Apache许可证和初版伯克利(后来修改版)许可证一样,但Apache2.0把二者区分开。这两者之间关键的区别:明确授予专利权:Apache许可证2.0明确规定,当使用、修改或发行Apache许可证下的软件时,授予专利权;它也列出了撤销授予的情况。
清晰定义使用概念:Apache 2.0 清晰定义它所使用的所有的条款和概念,几乎不会引起歧义。
重复使用,不用改写:Apache2.0能很容易的被其他项目使用,无需对许可证文档本身做任何改写。
自制光谱仪 theremino spectrometer
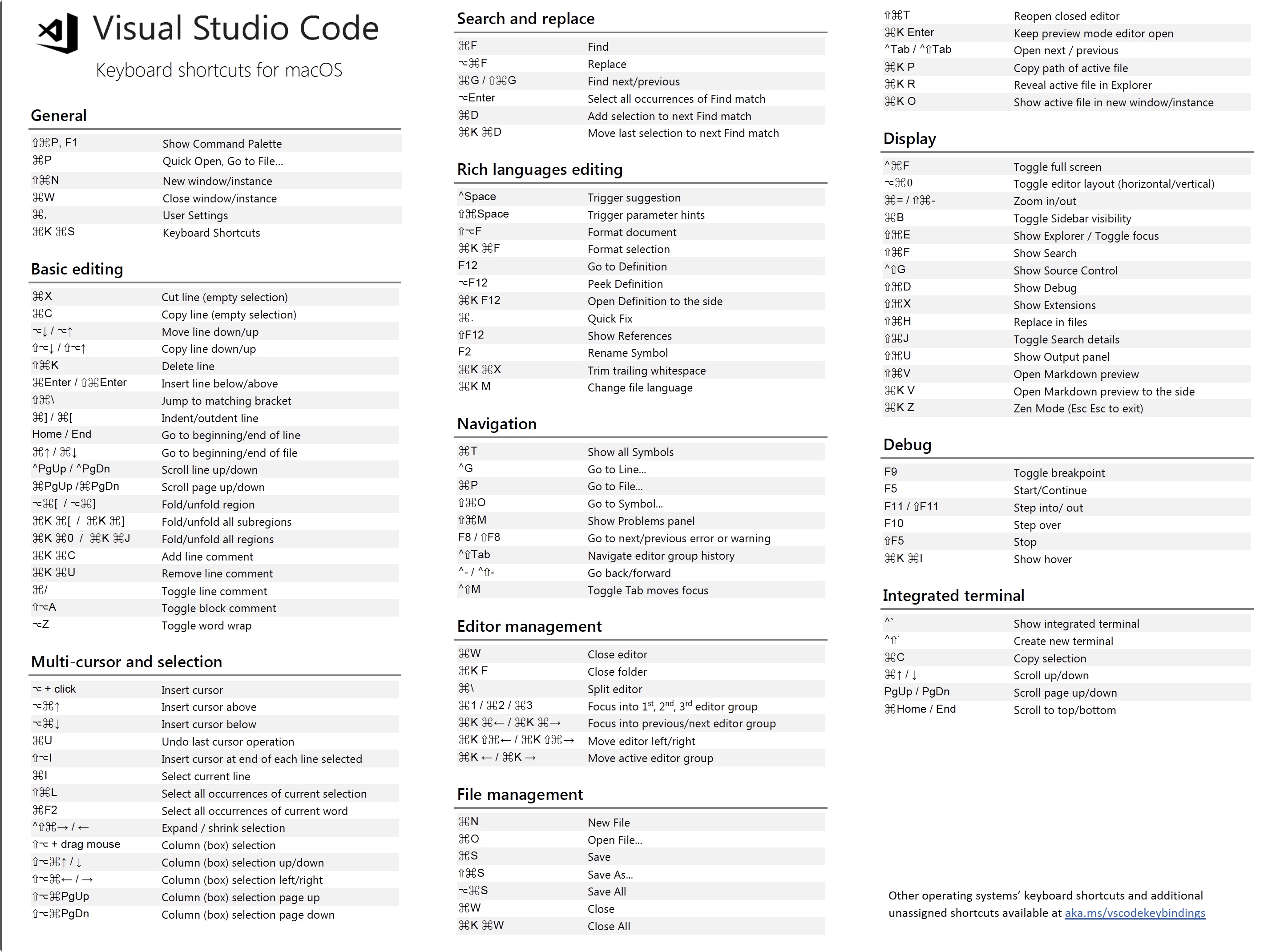
vscode快捷键
其中有漏的:
Ctrl+Shift+\ 在括号内时, 按一次跳转到括号的结尾, 再按一次跳到开头
发现一个模拟器linux
Blender入门之三
参考教程: Blender 商业广告教程 带你从头到尾的制作饮料广告
Cycles透镜研究
- 透镜为玻璃材质, 糙度0.
- 可以通过摄像头直接通过透镜看另一侧, 不能通过摄像头看光源通过透镜打在桌面上的光斑效果(桌面材质为原理化BSDF默认值)
*有影响最终效果的是渲染-光程-最多反弹次数
全反射镜(直角三棱镜)成功
使用5个全反射镜看文字, 旁边有一个点光源照亮文字.最多反弹次数中至少需要如下设置:
- 总数 15, 减1则看不到点光源的光线, 减2则黑.
- 光泽 5. 减1则黑.
- 透射 10, 减1则看不到点光源的光线, 减2则黑.
其他参数可以为0
导光板 (失败)
导光板为玻璃材质.
侧发光灯珠原理化BSDF默认值, 朝向导光板一侧为发光材质, 值1000.
扩散板为半透默认材质
导光板打点采用立方体原理化BSDF默认值, 略侵入导光板.
镜头直视扩散板一侧
- 漫射至少为1, 我设置为2
- 透射至少为2
- 光泽有一个较大值新效果更好, 我设置为12.
确实可以有导光板的效果, 然而半透材质的扩散板出光量要远远多于打点的出光量, 以至于打点的出光量可以忽略不计
注意
- 环状物不能使用两个柱体的布尔减生成, 因为柱体的上下面超过了四边形, 所以这种生成的上下面也有超过四边形的问题, 进行 倒角和细分都会有问题. 正确的做法是直接增加环, 或者使用面+螺旋修改器生成.
曲线
添加一个贝塞尔曲线以后进入编辑模式, 然后删除, 就可以用Ctrl+左键点击的方式增加点了
V 控制柄类型菜单
gcc/clang-cl中消除特定警告的方法
参考: http://www.136.la/tech/show-547510.html
简单来说, 就是打印的告警中会有类似[-Wpointer-sign]这样的内容, 在编译时加上参数-Wno-pointer-sign就行, 也就是在-W后面加上no-
磁盘迁移
目前有这么几个软件:
- AOMEI Backupper Standard
- clonezilla, Norton Ghost的开源版本
- rescuezilla, clonezilla的GUI版
启动盘制作工具
windows11上安装支持图形界面GUI的Ubuntu子系统
- 搜索
启用或关闭Windows功能, 启用适用于Linux的Windows子系统和虚拟机平台, 确定后需要重启一次; - 打开
Microsoft Store, 搜索Linux并安装Winddows subsysterm for linux preview和Ubuntu 22.04 LTS(或者其他版本) - 按提示安装完以后, 给Ubuntu换aliyun的源, 在ubuntu的bash里面安装
sudo apt install x11-apps - bash里试着运行
xeyes &,如果打开了说明GUI安装成功.
Blender学习资源
mac mini系统崩溃要恢复怎么办?
苹果官方文档:关于基于 Intel 的 Mac 电脑上的 macOS 恢复功能中写道
- 按住这两个按键:Command (⌘) 和 R 键开机即可. 使用普通键盘没有
⌘键, 在USB键盘上用Win键代替. 也就是长按Win+R
普通键盘与apple键盘对应关系,
| USB Windows键盘 | Apple键盘 |
|---|---|
| Ctrl | Control |
| Win | Command ⌘ |
| Alt | Option |
Apple社区问题: 如何重装Mac mini系统?中写的组合键有所不同,是Option-Command-R组合键, 也就是Alt+Win+R
在这个文章How to enter BIOS mode on Mac and what to do with it中提到, 长按Command-S开机可以进入类Unix界面解决系统问题.
选择启动盘的方法: 按住Alt开机